Sun Synchronous Orbit Ground Track


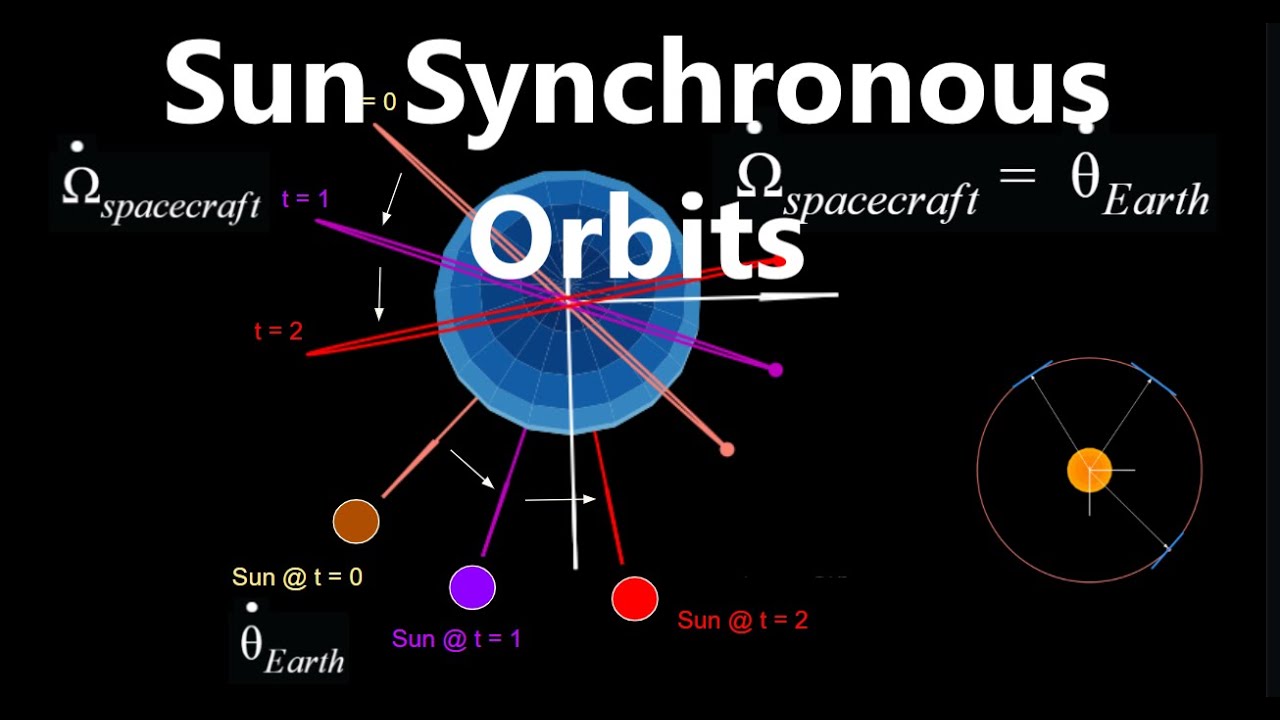
As another answer correctly stated, a Sun-Synchronous Orbit (SSO) with a Local Time of Ascending Node (LTAN) of 12 Noon would experience the maximum eclipse since the vector to the sun would lie within the orbital plane and an orbit with an LTAN of 11 AM would experience an eclipse time of close to that. The exact eclipse time could be. A sun-synchronous orbit (SSO), also called a heliosynchronous orbit, is a nearly polar orbit around a planet, in which the satellite passes over any given point of the planet's surface at the same local mean solar time. More technically, it is an orbit arranged so that it precesses through one compl.
A Sun-synchronous orbit (SSO, also called a helio-synchronous orbit) is a geocentric orbit that combines altitude and inclination in such a way that the satellite passes over any given point of the planet's surface at the same local solar time. Sun-synchronous orbit. An orbit in which the satellite's orbital plane is at a fixed orientation to the sun, i.e., the orbit precesses about the earth at the same rate that the earth orbits the sun. It has the characteristics of maintaining similar sun angles along its ground trace for all orbits, and typically has an inclination from 96 to 98.
Sun Synchronous Orbit Purpose
How to calculate the synchronous orbits of the planets?
The synchronous orbit planets is calculated using the law of universal gravitation which boils down to: h=√3(G*M*T2/4π2)-R
h = Height of the artificial satellite
G = Constant of gravitation (6.67*10-11)
M = Mass of the planet
T = Rotational period of the planet
R = Radius of the planet
The geosynchronous orbit (synchronous orbit of the Earth) is at an altitude of 35,796 km (≈ 36,000 km) and has a semi-major axis of 42,167 km.
Excel formula used in this table to calculate the altitude of the satellite in synchronous orbit of the planet:
=((((G*M*T^2)/(4*PI()^2))^(1/3))-R*1000)/1000
Excel formula used to calculate the semi-major axis of the synchronous orbit of the planet:
=((((G*M*T^2)/(4*PI()^2))^(1/3)))/1000